前几天有一个关注很久的公众号推送了一篇讲 “三门问题” 的文章。这不是我第一看到这个问题的分析,我一直觉得这个是个伪命题,后面两个门打开后面有大奖的概率都应该是1/2才对呀。直到我去看了一些分析,写了这篇文章。

什么是三门问题?
蒙提霍尔问题,亦称为蒙特霍问题或三门问题(英文:Monty Hall problem),是一个源自博弈论的数学游戏问题,大致出自美国的电视游戏节目Let’s Make a Deal。问题的名字来自该节目的主持人蒙蒂·霍尔。
这个游戏的玩法是:参赛者会看见三扇关闭了的门,其中一扇的后面有一辆汽车或者是奖品,选中后面有车的那扇门就可以赢得该汽车或奖品,而另外两扇门后面则各藏有一只山羊。当参赛者选定了一扇门,但未去开启它的时候,知道门后情形的节目主持人会开启剩下两扇门的其中一扇,露出其中一只山羊。主持人其后会问参赛者要不要换另一扇仍然关上的门。问题是:换另一扇门会否增加参赛者赢得汽车的几率?如果严格按照上述的条件的话,答案是会。换门的话,赢得汽车的几率是2/3。
这条问题亦被叫做蒙提霍尔悖论:虽然该问题的答案在逻辑上并不自相矛盾,但十分违反直觉。这问题曾引起一阵热烈的讨论。
理论证明
先说一下错误的思维方式:当主持人打开一扇后面有羊的门之后,问题就变成了有两扇门,一扇门里有汽车,一扇门里有羊,选择任何一个门获的汽车的概率必然是相同的,也就是1/2。
上面这种方式的问题就是,打开一扇门后,并不等价于在两扇门里做选择;而是你是否需要转换。(人的直觉往往是不可信的)
当年的玛丽莲·沃斯·莎凡特用整整4个专栏,数百个新闻故事及在小学生课堂模拟的测验来说服她的读者她是正确的。
我们只有最最简单的列出所有可能的情况就可以证明这个问题。
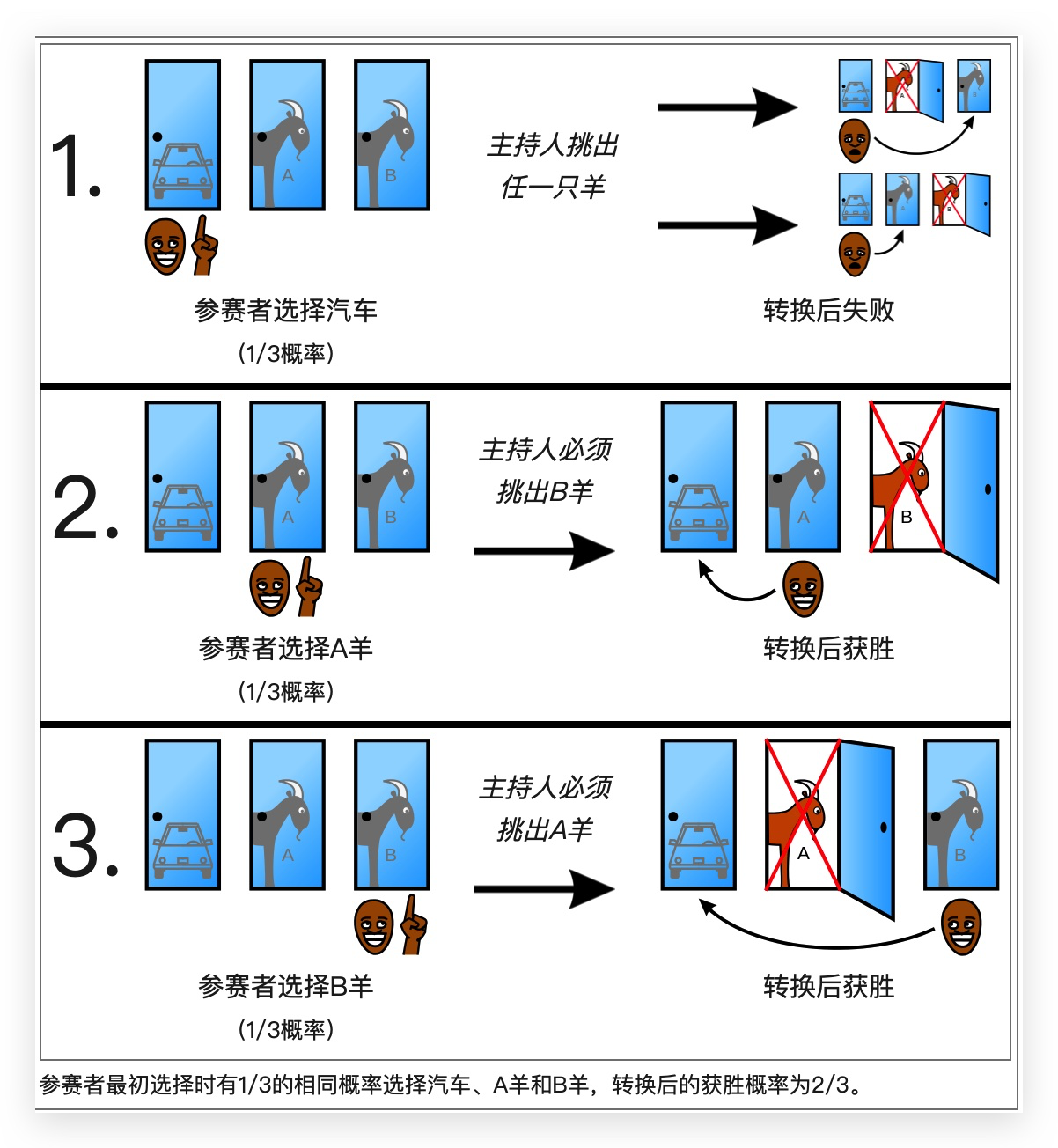
上图可以看到,转换后获胜的概率是2/3。
但是有质疑是为什么第一种情况下不可以分为 A 羊和 B 羊,而是算作一种情况呐。我认为这是由于打开门后出现 A 羊还是 B 羊,并不会影响我们计算的概率,影响概率的是主持人选羊这件事。所以 A 羊和 B 羊并不能算作两种情况。
代码佐证
概率问题通过增大样本容量来获取接近概率的值。所以不如写一段代码来看一下结果
🐑🐑 区分 A 羊和 B 羊
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| public class Main {
public static final boolean CAR = true;
public static final boolean GOAT_A = false;
public static final boolean GOAT_B = false;
public static void main(String[] args) throws ExecutionException, InterruptedException {
int changeSuccess = 0;
int totalCount = 100_0000;
List<List<Boolean>> lists = Arrays.asList(
Arrays.asList(CAR, GOAT_A, GOAT_B),
Arrays.asList(CAR, GOAT_B, GOAT_A),
Arrays.asList(GOAT_A, CAR, GOAT_B),
Arrays.asList(GOAT_A, GOAT_B, CAR),
Arrays.asList(GOAT_B, GOAT_A, CAR),
Arrays.asList(GOAT_B, CAR, GOAT_A));
ExecutorService executorService = Executors.newCachedThreadPool();
List<Future<Boolean>> resultList = new ArrayList<>();
for (int i = 0; i < totalCount; i++) {
Future<Boolean> resultFuture = executorService.submit(() -> {
int randomIndex = ((int) (Math.random() * 100)) % lists.size();
List<Boolean> doors = lists.get(randomIndex);
int firstChoose = ((int) (Math.random() * 100)) % 3;
int openDoorIndex = 0;
do {
openDoorIndex = ((int) (Math.random() * 100)) % 3;
} while (openDoorIndex == firstChoose || doors.get(openDoorIndex));
int secondChoose = 3 - firstChoose - openDoorIndex;
return doors.get(secondChoose);
});
resultList.add(resultFuture);
}
for (Future<Boolean> booleanFuture : resultList) {
Boolean aBoolean = booleanFuture.get();
if (aBoolean) {
changeSuccess++;
}
}
System.out.println("换选获胜次数:" + changeSuccess);
System.out.println("总次数:" + totalCount);
System.out.println("换选获胜几率:" + (changeSuccess * 1.0 / totalCount));
executorService.shutdown();
while (executorService.isTerminated()) {
executorService.awaitTermination(100, TimeUnit.SECONDS);
}
}
}
|
1
2
3
| 换选获胜次数:666072
总次数:1000000
换选获胜几率:0.666072
|
🐑 不区分两只羊
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
| public class Main2 {
public static final boolean CAR = true;
public static final boolean GOAT = false;
public static void main(String[] args) throws ExecutionException, InterruptedException {
int changeSuccess = 0;
int totalCount = 100_0000;
List<List<Boolean>> lists = Arrays.asList(
Arrays.asList(CAR, GOAT, GOAT),
Arrays.asList(GOAT, CAR, GOAT),
Arrays.asList(GOAT, GOAT, CAR));
ExecutorService executorService = Executors.newCachedThreadPool();
List<Future<Boolean>> resultList = new ArrayList<>();
for (int i = 0; i < totalCount; i++) {
Future<Boolean> resultFuture = executorService.submit(() -> {
int randomIndex = ((int) (Math.random() * 100)) % lists.size();
List<Boolean> doors = lists.get(randomIndex);
int firstChoose = ((int) (Math.random() * 100)) % 3;
int openDoorIndex = 0;
do {
openDoorIndex = ((int) (Math.random() * 100)) % 3;
} while (openDoorIndex == firstChoose || doors.get(openDoorIndex));
int secondChoose = 3 - firstChoose - openDoorIndex;
return doors.get(secondChoose);
});
resultList.add(resultFuture);
}
for (Future<Boolean> booleanFuture : resultList) {
Boolean aBoolean = booleanFuture.get();
if (aBoolean) {
changeSuccess++;
}
}
System.out.println("换选获胜次数:" + changeSuccess);
System.out.println("总次数:" + totalCount);
System.out.println("换选获胜几率:" + (changeSuccess * 1.0 / totalCount));
executorService.shutdown();
while (executorService.isTerminated()) {
executorService.awaitTermination(100, TimeUnit.SECONDS);
}
}
}
|
1
2
3
| 换选获胜次数:665600
总次数:1000000
换选获胜几率:0.6656
|
参考
蒙提霍尔问题 - 维基百科,自由的百科全书

