如何解决动态规划问题

技术

曾经的我以为动态规划很神秘，很难理解。后来随着刷的动态规划相关的题越来越多，对于动态规划也就驾轻就熟了。我一开始来认识动态规划是通过概念来理解的，这对于我来说总是显得晦涩。我不是一个善于死记理论的人，反而是通过多刷题，回头再去看动态规划的使用情况则是有一种恍然大悟感。这样的获得想必也不会轻易忘记。刷题并不能让人变得聪明，但确实能够锻炼一个人的思维。

img

递归 + 数组 = 动态规划

先看一眼概念也未必是坏事：动态规划 - 维基百科，自由的百科全书

动态规划的所有题目，在不考虑性能的情况下，都可以使用简单的递归来解决。

题目

下面来看一道 LeetCode 经典动态规划题目：(70) Climbing Stairs - LeetCode

You are climbing a stair case. It takes n steps to reach to the top.

Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

Note: Given n will be a positive integer.

Example 1:

1
2
3
4
5
Input: 2
Output: 2
Explanation: There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps

Example 2:

1
2
3
4
5
6
Input: 3
Output: 3
Explanation: There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step

递归

公式如下（这个也是做动态规划必须要列出的公式）
$$
f(n)=\begin{cases}
n,\quad n\leq 2 \\
f(n-1)+f(n-2),\quad x>2
\end{cases}
$$
我们来试试用简单的递归来解决这个问题：

1
2
3
4
5
6
7
8
9
10
11
/**
 * Created by jacob on 2019-08-20.
 */
public class Solution {
    public int climbStairs(int n) {
        if (n <= 2) { // 递归终结点
            return n;
        }
        return climbStairs(n - 1) + climbStairs(n - 2);
    }
}

如果我们这时候计算的是 climbStairs(5)，通过下图可以看到我们一共计算 f(3) 2次、 f(2) 3次、 f(1) 2次。这是在台阶数 n 很小的情况下，如果 n 很大的话，重复计算的模块会变的更多。

DP

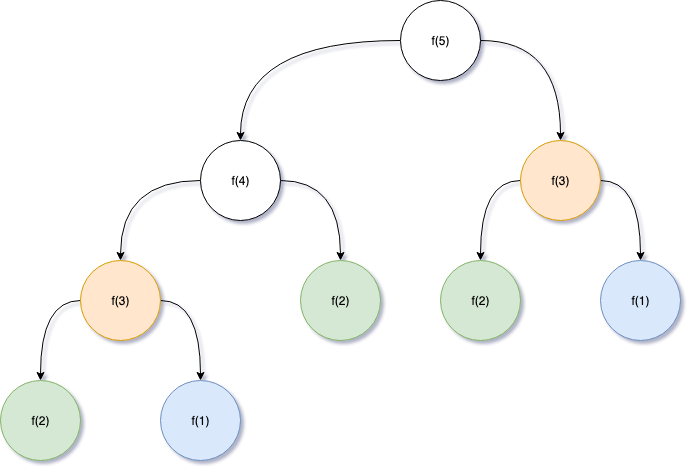
数组记录中间结果

这个时候如果我们能够通过一个数组来记录中间结果就好了，当上图中的每一个节点如果已经计算过，就不再重复计算了。

DP2

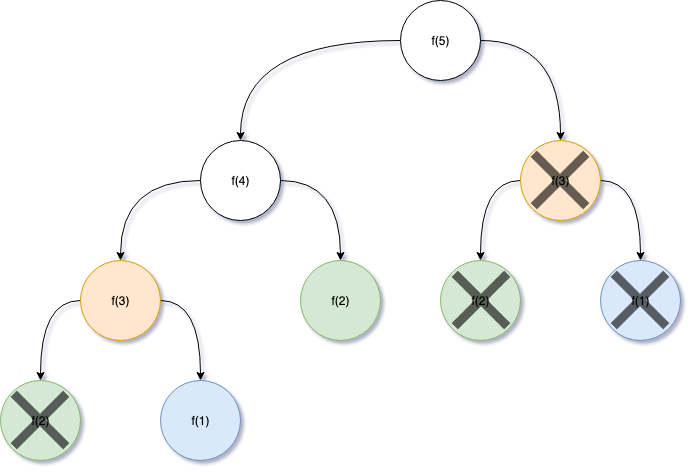
代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int climbStairs(int n) {
        int[] dp = new int[n + 1];
        return this.climbStairs(dp, n);
    }

    private int climbStairs(int[] dp, int n) {
        if (n <= 1) {
            return 1;
        }
        if (dp[n] > 0) {
            return dp[n];
        }
        int num = climbStairs(dp, n - 1) + climbStairs(dp, n - 2);
        dp[n] = num;
        return num;
    }
}

去掉递归

递归会新建很多局部变量，建立很多栈帧，带来很多不必要的消耗，如果能够去除递归效率会有进一步的提升。
$$
f(n)=\begin{cases}
n,\quad n\leq 2 \\
f(n-1)+f(n-2),\quad x>2
\end{cases}
$$
上面我们都是从图中的根结点一步一步向下计算，是一个深度优先搜索的过程，如果我们从根节点向上算就能去掉递归了。

DP-3

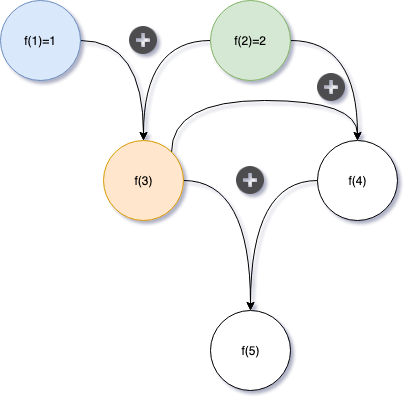
代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/**
 * Created by jacob on 2019-08-20.
 */
public class Solution2 {
    public int climbStairs(int n) {
        int[] dp = new int[n + 1];
        for (int i = 1; i <= n; i++) {
            if (i <= 2) {
                dp[i] = i;
            } else {
                dp[i] = dp[i - 1] + dp[i - 2];
            }
        }
        return dp[n];
    }
}

动态规划题目

多刷点题，就啥都明白了。